Na wypadek awarii

W ramach wakacyjnego relaksu proponuję zadanie z zawodów Central European Programming Contest organizowanych osiem lat temu przez Instytut Informatyki Uniwersytetu Wrocławskiego. Zadanie jest oczywiście z geometrii, ale tym razem w tylko dwóch wymiarach: dostajemy punktów na płaszczyźnie, dla każdego z nich chcemy znaleźć najbliższego sąsiada. Odległość jest standardowa, to znaczy euklidesowa.

Oryginalną treść można zobaczyć na przykład tutaj, można tam także sprawdzić swoje rozwiązanie. Jedynym szczegółem, na który być może warto zwrócić uwagę, jest obietnica, że podane punkty nie powtarzają się (oraz , więc zadanie jest dobrze zdefiniowane).

Każdy choćby średnio doświadczony zawodnik po przeczytaniu treści pewnie od razu pomyślał o klasycznej wersji, w której szukamy pary najbliższych punktów. Jeśli potrafilibyśmy szybko znaleźć najbliższego sąsiada dla każdego punktu to oczywiście łatwo moglibyśmy wyznaczyć taką parę, warto więc przypomnieć sobie jak rozwiązuję się tę prostszą (i bardziej znaną) wersję w czasie .

Są przynajmniej dwa sposoby. Obydwa korzystają z podobnej obserwacji, ale jeden stosuje strategię dziel-i-zwyciężaj, a drugi zamiatanie. Ten drugi jest pewnie nieco łatwiejszy w implementacji, jednak dla nas bardziej przydatny będzie ten pierwszy.

Podzielmy płaszczyznę na dwie części prostą pionową tak, aby w każdej z otrzymanych dwóch części znalazła się mniej więcej połowa wszystkich punktów. (Załóżmy na razie, że wszystkie punkty mają różne współrzędne i taki podział jest możliwy.) Rekurencyjnie znajdźmy parę najbliższych punktów na lewo od prostej oraz parę najbliższych punktów na prawo, niech oznacza minimum ze znalezionych w ten sposób odległości. Być może jest już poprawną odpowiedzią dla całego problemu, jednak może się także zdarzyć, że ta odpowiedź jest wyznaczona przez punkty leżące po różnych stronach prostej. Zauważmy jednak, że w takim przypadku jeden z tych punktów jest postaci gdzie , a drugi dla . Innymi słowy: możemy spokojnie usunąć wszystkie punkty leżące poza pasem szerokości . Co dalej?

Ustalmy . Zauważmy, że wszystkie punkty , których wybranie mogłoby prowadzić do polepszenia odpowiedzi, spełniają nie tylko lecz również . Ile może być takich punktów?

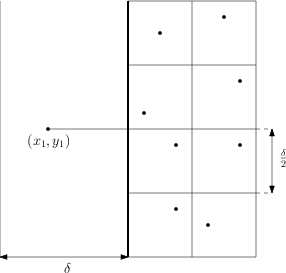
Nie za dużo: co najwyżej jeden w każdym z kwadratów na powyższym rysunku. Gdyby bowiem dwa z nich leżały w tym samym kwadracie to byłyby w odległości nie większej niż . Fajnie, pokazaliśmy więc, że dla każdego punktu po lewej mamy tylko kilku sensownych kandydatów na punkt po prawej, który należy rozważyć jako być może poprawiający odpowiedź. Ale jak szybko dobrać się do tych kilku kandydatów?

Posortujmy wszystkie punkty z lewej , dla których , względem współrzędnej . Podobnie, posortujmy wszystkie punkty z prawej , dla których , względem współrzędnej . Teraz zauważmy, że dla każdego punktu z lewej wystarczy znaleźć pierwszy punkt z prawej na naszej posortowanej liście, dla którego : wszyscy kandydaci mogą być wtedy wygenerowani biorąc jego kilku poprzedników i kilku następników. Jak szybko znaleźć ten pierwszy punkt z prawej? Wystarczy przesuwać dwa palce po obydwu posortowanych listach, co wymaga w sumie tylko czasu liniowego. Ignorując więc konieczność posortowania punktów, czas działania całego rozwiązania jest opisany przez rekurencję , czyli . Niestety, nie do końca możemy zignorować tę konieczność. Na szczęście dość łatwo jednak uniknąć zwiększenie złożoności do stosując prosty trik: sortujemy wszystkie punkty raz a dobrze względem współrzędnej . Następnie w każdym wywołaniu rekurencyjnym zakładamy, że dostaliśmy tak posortowane punkty. Łatwo widać, że możemy utrzymywać taki porządek dzieląc punkty na lewe i prawe. Jest jeszcze jeden szczegół: chcemy wybrać prostą pionową dzielącą punkty na dwie mniej więcej równe grupy. W tym celu można pewnie wybrać medianę wszystkich współrzędnych , co jest trywialne jeśli są one posortowane względem współrzędnej . Tak naprawdę przekazujemy więc dwie listy, obydwie zawierające ten sam zbiór punktów: jedna jest posortowana względem współrzędnej , a druga względem współrzędnej .

Skoro przypomnieliśmy już sobie jak rozwiązać prostszą wersję zadania, wróćmy do tej trudniejszej. Naturalne wydaje się zastosowanie podobnej metody, to znaczy wybranie prostej pionowej dzielącej punkty na dwie mniej więcej równe grupy i uruchomienie się rekurencyjnie dla wszystkich punktów po lewej i wszystkich punktów po prawej. Teraz jednak wynikiem takiego wywołania nie jest jedna liczba: dla każdego punktu dostajemy jego odległość do najbliższego sąsiada . Być może wywołanie rekurencyjne wystarczy, żeby poprawnie wyznaczyć , może być jednak i tak, że najbliższy sąsiad punktu po lewej jest punktem po prawej (lub na odwrót). Sytuacja jest symetryczna, skupmy się więc na „naprawieniu” sytuacji dla każdego punktu po lewej. Chcemy więc sprawdzić, czy przypadkiem nie ma punktu po prawej , dla którego . Ale jak?

Kuszące wydaje się ograniczenie liczby kandydatów, których należy rozważyć dla każdego takiego punktu z lewej. Zauważmy więc, że jest sensownym kandydatem tylko jeśli przecięcie okręgu o środku w i promieniu z prostą zawiera punkt tak jak na poniższej ilustracji.

Czy potrafilibyśmy ograniczyć liczbę takich kandydatów? Wydaje się, że nie bardzo: może się zdarzyć, że jeden punkt z lewej będzie miał ich wielu. Ale może dałoby się ograniczyć ich sumaryczną liczbę? Lub, mówiąc inaczej, może dałoby się ograniczyć liczbę punktów z lewej, dla których dany punkt z prawej jest sensownym kandydatem? Spróbujmy!

Załóżmy, że punkt z prawej strony jest sensownym kandydatem dla 4 punktów z lewej strony. Podzielmy lewą część płaszczyzny na 3 kawałki tak jak poniżej.

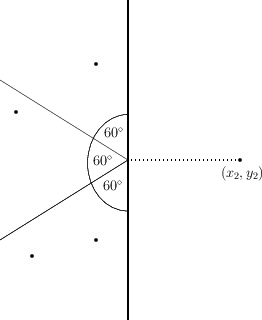
W jednej z tych części mamy 2 punkty z lewej strony, oznaczmy je oraz . Zauważmy, że kąt wyznaczony przez jest nie większy niż 60 stopni, oznaczmy go przez . Tak naprawdę chcielibyśmy założyć, że : wymaga to zdefiniowania kawałków tak, aby były jednostronnie domknięte i założenia, żew wszystkie punkty po lewej są ściśle na lewo od prostej . Mamy więc trójkąt o dwóch bokach długości i kącie między nimi. Długość trzeciego boku to po prostu odległość między oraz , która nie może być mniejsza niż (bo przecież w przeciwnym wypadku wyznaczone odległości nie byłyby poprawne!). Korzystając z prawa kosinusów i zakładając bez straty ogólności, że dostajemy więc, że , więc po uproszczeniu . To jest jednak sprzeczność z założeniem, że .

No dobrze, czyli pokazaliśmy, że sumaryczna liczba kandydatów jest liniowa. Ale, znów, jak ich wygenerować? Prawie tak samo jak poprzednio: sortujemy punkty po lewej i punkty po prawej względem ich współrzędnych . Dla każdego punktu po lewej przeglądamy wszystkie punkty po prawej, których współrzędne mieszczą się w odpowiednim zakresie. Zauważmy, że należy do tego zakresu, więc znając punkt po prawej z najmniejszą współrzędną jesteśmy w stanie wygenerować wszystkie takie punkty w czasie proporcjonalnym do ich licby. Tak jak w prostszej wersji zadania, możemy uniknąć sortowania utrzymując dwie kopie listy punktów i otrzymać rozwiązanie, które działa w czasie .

Wypada jeszcze wrócić do założenia, że wszystkie punkty mają różne współrzędne . Jeśli tak nie jest, nie zawsze istnieje prosta pionowa dzieląca je na dwie z grubsza równe grupy. Prosta nie musi być jednak pionowa: można ją lekko "kopnąć". Tak naprawdę oznacza to, że można posortować punkty leksykograficznie i wywołać się rekurencyjnie dla pierwszej i drugiej połówki tak posortowanej listy.

Warto także zastanowić się, czy nasze rozwiązanie jest optymalne. Nietrudno pokazać, że i owszem, jeśli dopuszczamy tylko podstawowe operacje arytmetyczne dla współrzędnych (a konkretniej: testy liniowe). Jeśli jednak dopuścimy także używanie podłogi (zaokrąglania) to można skonstruować algorytm, który działa w czasie . Jeśli zaś dopuścimy także randomizację: istnieje algorytm liniowy! Czy którekolwiek z tych szybszych rozwiązań uogólnia się do naszej wersji zadania?