Artykuł

Zadania z teorii liczb przedstawione w poprzednim odcinku chyba nie wzbudziły Waszego entuzjazmu, spróbujmy więc czegoś z teorii grafów. Tematyka o tyle lepsza, że aż prosi się o rysunki, a rysunki – wiadomo – są fajne. Trochę mniej fajnie, że twierdzenia z tej działki często wymagają dość żmudnego rozważenia kilku(nastu) przypadków, ale spokojnie, nie zawsze jest aż tak tragicznie. Jako przykład proponuję zadanie A z NEERC Western Subregional Contest 2012. Dostajemy w nim dość specyficzny graf nieskierowany, w którym podgraf indukowany przez sąsiadów dowolnego wierzchołka jest spójny, a ponadto nie ma tam (ciągle mówimy o podgrafie indukowanym przez sąsiadów dowolnego wierzchołka) antytrójkątów. Chcemy skonstruować jak najdłuższy cykl przechodzący przez wierzchołek numer . Warunki nałożone na graf ewidentnie sugerują, że… hmm?

W sumie ciężko powiedzieć, co sugerują te warunki. Są one jednak na tyle dziwaczne, że można na przykład podejrzewać taki graf o bycie hamiltonowskim (no, lub bycie niespójnym, ale przecież każdy szanujący się graf jest spójny), czyli o to, że zawsze można znaleźć w nim cykl przechodzący przez każdy wierzchołek dokładnie raz. Okazuje się, że faktycznie tak jest! Jednak zanim zabierzemy się za skonstruowanie (konstruktywnego!) dowodu tego podejrzenia, zastanówmy się przez chwilę nad czymś zupełnie innym. No, może nie zupełnie, ale trochę.

Powiedzmy, że mamy dany graf (znów nieskierowany) na wierzchołkach, w którym stopień każdego wierzchołka to przynajmniej . Okazuje się, że taki warunek wystarcza, żeby można było efektywnie skonstruować cykl, który przechodzi przez każdy wierzchołek dokładnie raz. Pewnie można to udowodnić na kilka różnych sposobów, ale taki najbardziej standardowy polega na stopniowym konstruowaniu coraz dłuższych cykli prostych (czyli takich, na których wierzchołki i krawędzie nie powtarzają się). Na dobry początek możemy wybrać dowolny cykl prosty. Jeśli takiego nie ma, to nasz graf jest drzewem, czyli jest w nim przynajmniej jeden wierzchołek stopnia , czyli sprzeczność. Następnie spróbujmy pokazać, że dysponując cyklem prostym o długości umiemy (szybko) skonstruować cykl prosty o długości (lub więcej).

Najpierw spróbujmy jednak (też szybko) skonstruować ścieżkę prostą o takiej długości. W najprostszy możliwy sposób: próbujemy znaleźć , który nie leży na cyklu, ale jest sąsiadem jakiegoś , wtedy ścieżka to po prosty . Jeśli takiego nie ma, to cały cykl stanowi jedną spójną składową, czyli jest jeszcze jakaś inna spójna składowa, czyli jedna z nich ma rozmiar . Ale wtedy wierzchołki w niej nie mogą być stopnia przynajmniej !

Teraz mając ścieżkę prostą długości spróbujmy skonstruować cykl prosty o przynajmniej takiej samej długości. Jeśli i są sąsiadami, nasza ścieżka jest tak naprawdę cyklem, załóżmy więc przeciwnie. Jeśli lub mają sąsiada poza ścieżką, można wydłużyć ścieżkę o jeden wierzchołek i powtórzyć rozumowanie, załóżmy więc, że tak nie jest. Wtedy wszyscy sąsiedzi i należą do . Ale skoro każdy z nich ma przynajmniej sąsiadów, istnieje dla którego jest sąsiadem , a jest sąsiadem . Wtedy zaś szukanym cyklem jest:

Przy odrobinie ostrożności całą procedurę można zaimplementować w czasie na każde rozszerzenie o jeden.

Z braku lepszych pomysłów możemy spróbować zastosować opisaną wyżej metodę stopniowego rozszerzania cyklu do naszego zadania. Niestety po drodze napotkamy pewne trudności, ale to nawet lepiej. Przynajmniej będzie ciekawie.

Mamy dany spójny graf nieskierowany na wierzchołkach, w którym podgraf indukowany przez sąsiadów dowolnego wierzchołka jest spójny, a ponadto nie ma tam antytrójkątów. Chcemy pokazać, że mając w takim grafie cykl prosty długości , jesteśmy w stanie (szybko) skonstruowac cykl prosty długości . Jest to dość ambitnie zamierzenie, więc może zacznijmy od skromnej obserwacji: jeśli , graf na pewno zawiera jakiś cykl prosty (prosty oznacza tutaj tyle, że zarówno wierzchołki jak i krawędzie nie mogą się powtarzać; w szczególności, pojedyncza krawędź nie jest cyklem prostym). Załóżmy, że jest przeciwnie, czyli graf jest drzewem. Ale wtedy istnieje w nim wierzchołek stopnia przynajmniej . Wybierzmy dwóch jego sąsiadów i nazwijmy ich i . Z założenia o spójności podgrafu indukowanego przez sąsiadów otrzymujemy, że istnieje ścieżka łącząca z , która omija . Dorzucając do tej ścieżki otrzymamy żądany cykl prosty.

Załóżmy, że mamy już cykl prosty długości . Naszym celem będzie wydłużenie go, przy czym w przeciwieństwie do prostszej wersji opisanej powyżej, niekoniecznie tylko dodając wierzchołek. Również w przeciwieństwie do prostszej wersji, rzeczone wydłużenie będzie wymagało odrobiny zastanowienia. Zacznijmy od prostej obserwacji: skoro , na pewno przynajmniej jeden z wierzchołków na cyklu ma sąsiada poza cyklem. Dla ustalenia uwagi powiedzmy, że ma sąsiada , który nie leży na cyklu. No, może i nie leży on na cyklu, ale skoro podobnie jak jest sąsiadem , to na pewno istnieje ścieżka łącząca i , tak jak na poniższej ilustracji, która w dodatku przechodzi tylko przez sąsiadów .

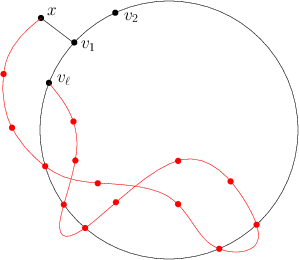
Wybierzmy sobie najkrótszą z takich ścieżek. Jest to dość częsty trik w tego typu dowodach: zamiast patrzeć na dowolne rozwiązanie, o którym ciężko cokolwiek powiedzieć, patrzymy na (w jakimś sensie) najmniejsze, którego struktura nie może być już tak zupełnie dowolna. Okazuje się, że ta najkrótsza ścieżka nie może zawierać trzech wierzchołków wewnętrznych (wewnętrznych, czyli tych ściśle między a ). Załóżmy bowiem, że są takie trzy wierzchołki. Wszystkie z nich są sąsiadami , czyli nie może być tak, że tworzą one antytrójkąt. Ale wobec tego jedna z wykropkowanych (poniżej) krawędzi musi faktycznie być krawędzią, no a to oznacza, że możemy jej użyć do skrócenia ścieżki.

No i pięknie. Mamy więc dwa przypadki: ścieżka zawiera dokładnie jeden wierzchołek wewnętrzny lub dokładnie dwa wierzchołki wewnętrzne. No, pewnie może być też i tak, że ścieżka składa się tylko z i , ale w takim wypadku możemy od razu wydłużyć cykl. Podobnie możemy postąpić mając krawędź  lub , czyli bez straty ogólności możemy założyć, że takich krawędzi nie ma. A to oznacza, z założenia o braku antytrójkątów wśród sąsiadów , że mamy krawędź . Ten trik warto dokładnie prześledzić, bowiem przyda się nam jeszcze nie raz, nie dwa, lecz aż trzy razy. Nie mniej i nie więcej.

Zacznijmy od przypadku, w którym ścieżka zawiera dokładnie jeden wierzchołek wewnętrzny. Pewnie okaże się on prostszy niż ten drugi, choć.. kto wie. Na pewno możemy jednak założyc, że ten unikalny wierzchołek wewnętrzny tak naprawdę jest jednym z , w przeciwnym wypadku moglibyśmy bowiem od razu wydłużyć cykl.

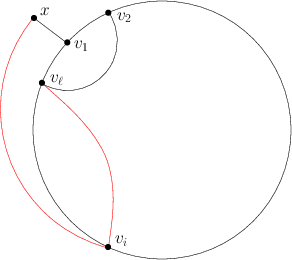
Popatrzmy na i (dla spokoju sumienia zauważmy, że żaden z nich nie jest wierzchołkiem ). Są to, podobnie jak , sąsiedzi , więc znów możemy skorzystać z założenia o braku antytrójkątów. W zamian dostajemy przynajmniej jedną z krawędzi , i . Teraz jest już łatwo: mając krawędź lub oraz możemy łatwo rozszerzyć cykl. Czyli pozostaje tylko poradzić sobie w sytuacji, gdy mamy tylko krawędź . Okazuje się to jednak być dość łatwe, jak widać poniżej.

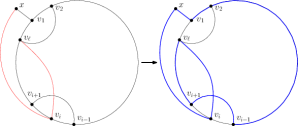
OK, to nie było takie trudne. No to zajmijmy się bardziej skomplikowanym przypadkiem, w którym ścieżka zawiera dokładnie dwa wierzchołki wewnętrzne. Podobnie jak wcześniej, przynajmniej jeden z tych dwóch wierzchołków musi tak naprawdę być jednym z . Niestety nie do końca wiadomo, czy dotyczy to tego pierwszego, tego drugiego, czy też może obydwu. Rozważmy sobie najpierw ten ostatni przypadek.

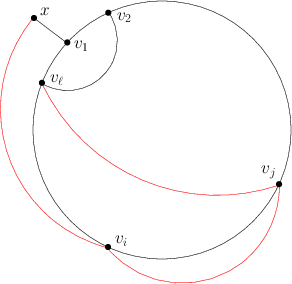
Powyższa ilustracja jest odrobinę tendencyjna: wcale nie mamy gwarancji, że i występują właśnie w takiej kolejności na cyklu. Ale nic to. Powtarzając rozumowanie o braku antytrójkątów dla , i , które wszystkie są sąsiadami , otrzymamy, że albo możemy łatwo rozszerzyć cykl o , albo mamy krawędź . A to oznacza, że możemy usunąć z naszego cyklu i zredukować sytuację do przypadku, gdy ścieżka najpierw przechodzi przez wierzchołek spoza cyklu, a następnie przez . No, prawie: trzeba będzie tylko zadbać o to, żeby nasze rozszerzanie przypadkiem nie skończyło się na dorzuceniu do cyklu tylko jednego wierzchołka. Byłoby to dość, hm, bezużyteczne. Trzeba również ponownie zadbać o sprawdzenie, czy jest krawędzią, mogło się bowiem zdarzyć, że lub był wierzchołkiem, który usuwamy z cyklu. Patrząc na sytuację w trochę bardziej optymistyczny sposób, w żadnym miejscu nie skorzystaliśmy z założenia, że drugi wewnętrzny wierzchołek to jakiś , czyli tak naprawdę załatwiliśmy dwa z trzech możliwych przypadków. Został nam już tylko jeden!

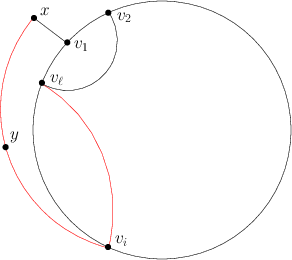
Załóżmy teraz, że ścieżka najpierw przechodzi przez wierzchołek , który nie leży na cyklu, a następnie przez . Po raz kolejny powtarzając rozumowanie o braku antytrójkątów dla , i , które wszystkie są sąsiadami dostaniemy przynajmniej jedną z krawędzi , , . Mając jedną z tych dwóch pierwszych krawędzi i przypominając sobie, że (jako wierzchołek na ścieżce) musi być sąsiadem , możemy dość łatwo rozszerzyć cykl, jak widać poniżej.

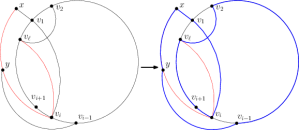
Przyjmijmy więc, że dysponujemy tylko . Wtedy jest jednak równie łatwo! (Uważny Czytelnik pewnie od razu zauważy, że mamy wtedy w zasadzie taką samą sytuację jak ta dla ścieżki składającej się z tylko jednego wierzchołka wewnętrznego; mam jednak nadzieję, że wybaczy mi ten recykling obrazków)

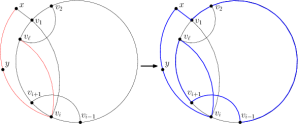
I.. i koniec. Rozważyliśmy wszystkie możliwe sytuacje, w każdej z nich udało nam się rozszerzyć cykl. Czynność należy powtórzyć, i prędzej lub później napawać się widokiem cyklu hamiltona. Trzeba by się tylko chwilę zastanowić nad kosztem całego przedsięwzięcia. Rozszerzenie cyklu wymaga tylko stałej liczby operacji, o ile mamy w ręce najkrótszą ścieżkę łączącą i w podgrafie indukowanym przez sąsiadów . Taką ścieżkę pewnie łatwo znaleźć używając choćby przeszukiwania wszerz, i dostać sumaryczną złożoność . Ale może da się lepiej?

Czasami pewnie się da. Graf z treści zadania jest dość rzadki (, ale ), pewnie warto by więc spróbować uzyskać złożoność, która jest lepsza niż dla . Równie naturalne wydaje się próba zbicia złożoności dla grafów gęstych, czyli dla . Wrócimy do tego tematu w jednym z kolejnych odcinków.